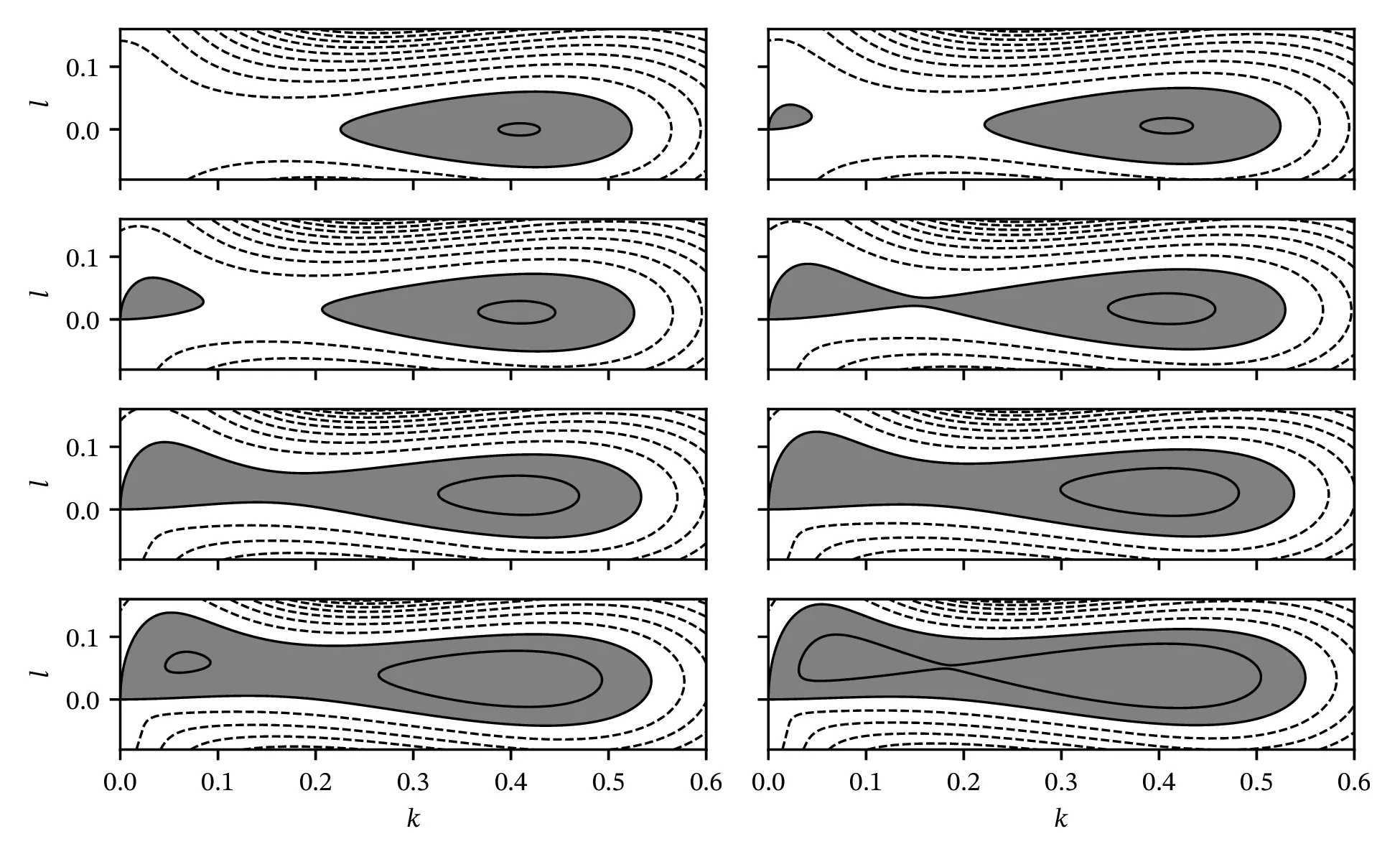
Stability analysis is performed on surface quasigeostrophic systems subjected to a Kolmogorov-type “shear force” on the boundaries using linear and nonlinear approaches. For a SQG system of semi-infinite depth forced on the upper boundary, the most linearly unstable mode is $2.74$ the energy injection length scale. This is contrary to two-dimensional fluid systems, where the linear instability is greatest for long waves. In the presence of damping, the most linearly unstable mode shifts toward shorter length scales. The nonlinear critical Reynolds number across different damping strengths is found to be qualitatively similar to that of Euler 2D systems. For an SQG system of finite thickness being forced on both boundaries, its behaviour approaches that of a semi-infinite SQG system at the large thickness limit. In the small thickness limit, the behaviour of a symmetrically forced fluid layer approaches that of a 2D system, while an antisymmetrically forced fluid layer is not susceptible to both linear and nonlinear instabilities. With ageostrophic effects, an SQG+ system of semi-infinite depth is much more prone to instabilities than an otherwise identical SQG system in the absence of damping due to the instability of long-wave modes. However, damping significantly suppresses such instabilities. With increasing damping, the most linearly unstable mode moves toward a smaller length scale. Contrary to the zero damping case, when the damping is sufficiently large, ageostrophic effects have a small but measurable stabilising effect.

Recommended citation: M. Lee and S. G. Llewellyn Smith, Stability of SQG Kolmogorov Flow, https://arxiv.org/abs/2511.10904, Nov. 2025, submitted.